CodeVita is the TCS Global Coding Contest for Students. First season of CodeVita was held in 2012 in India with an aim to spread the awareness on the various applications and use of coding.
CodeVita Season 9 Round 2 was conducted on 6th Feb, 2021, 03:30 UTC to 7th Feb, 2021, 03:30 UTC.
Total 8 questions was there in CodeVita Season 9 Qualifier Round (Round 2).
Students can code in 8 different programming languages.
| Language | Compiler / Interpreter Versions |
|---|---|
| C | gcc 8.3.1 |
| C++ | g++ 8.3.1 |
| C# | mono 6.8.0.123 |
| Java | Open jdk 1.8 |
| Perl | 5.26.3 |
| PHP | 7.2.11 |
| Python | Python 3.6 |
| Ruby | 2.7.1 |
First 4 questions are in this post and last 4 questions are in the next post(Link at the end of this post).
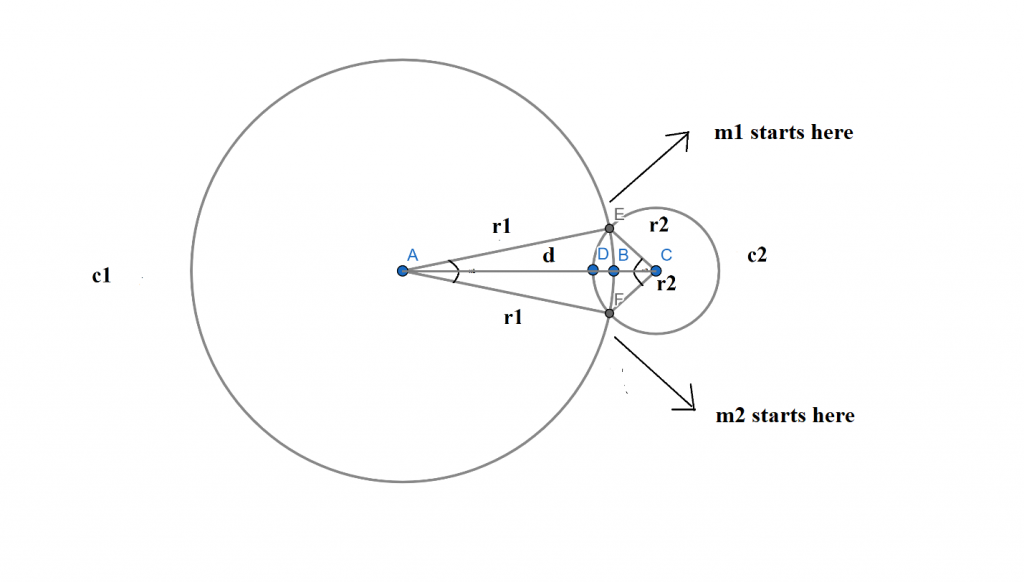
1) Circular Tracks
Problem Description
There are two circular tracks (C1 and C2) on which two motorcyclists (m1 and m2) are moving with two different speeds (s1, s2 m/s) (+ve for clockwise movement and -ve for anti-clockwise movement)
The radius of the tracks are r1 and r2 meters and d is the distance between their centers.
Your job is to compute if they will crash in given time t seconds, if m1 starts from E and m2 starts from F, where t is the time after which motorcycles will stop.
If yes, then find the time of the first crash and the collision point viz. {E, F}. If E and F coincide with each other, then consider first crash after 0 seconds.
For safety sake, if m1 and m2 reach the same point viz. {E, F} in the same second but a few milliseconds apart consider that as a crash. For example, if m1 crosses E at 5.66666231 second and m2 crosses E at 5.89544578 second, consider that both crash at the 5th second.
If there is no crash print ‘no crash’.
Constraints
All the inputs are integers.
Assume pi=3.141592653589793
Input
First line contains an integer r1, which represents radius of circular track C1 in meters.
Second line contains an integer r2, which represents radius of circular track C2 in meters.
Third line contains an integer s1, which represents the speed of m1 in m/s.
Fourth line contains an integer s2, which represents the speed of m2 in m/s.
Fifth line contains an integer t, which represents time in seconds after which the motorcycles will stop.
Sixth line contains an integer d, which represents distance between the centers of circles C1 and C2.
Output
One line containing the second at which the crash occurs along with the point at which the crash happens i.e. E or F, in the format,
<second of crash> <space> <E/F>.
If crash happens at either E or F. For example, if the motorcycles crash at 10th second at point E, then print “10 E”.
If the points E and F are coinciding then print “<second of crash> <space> <E&F>” (Refer Example 2).
If no crash happens then print “no crash”.
Time Limit
1Examples
Example1
Input
20
6
8
5
60
23Output
47 EExplanation
As per the inputs, circle1 (radius = 20 m, speed = 8m/s (clockwise)), circle2 (radius = 6 m, speed = 5 m/s (clockwise))
Time t after which motorcycles will stop = 60 sec.
Distance between the centers is 23 m.
m1 crosses E at 15.707963267948967, 31.415926535897935, 47.12388980384691 seconds respectively.
m2 crosses E at 2.2320236380400553, 9.77184600665556, 17.311668375271065, 24.85149074388657, 32.391313112502075, 39.93113548111758, 47.47095784973308, 55.010780218348586 seconds respectively
m1 crosses F at 1.2143415782596505, 16.92230484620862, 32.63026811415759, 48.33823138210656 seconds respectively
m2 crosses F at 7.539822368615504, 15.079644737231009, 22.619467105846514, 30.159289474462017, 37.699111843077524, 45.23893421169303, 52.77875658030853 seconds respectively
From above we can see that both motorcycles m1 and m2 are at point E in the 47th second. Hence they are deemed to crash at 47th second. Hence the output is “47 E”
Example 2
Input
4
4
5
5
60
8Output
5 E&FExplanation
Since the difference between the centers is equal to r1+r2, hence the tracks will have only 1 common point.
Since both motorcycles pass at 5.026548245743669 second from the same common point, hence the output is “5 E&F“
2) Skip Station
Problem Description
Codu wants to travel from City A to City B. There are N stations between A and B. There are 3 kinds of trains that run from every station.
Train 1- Stops at every station
Train 2- Stops at every alternate station
Train 3- Stops at every third station
Codu can use any combination of the trains to reach from City A to City B. However, he cannot travel in the reverse direction during the course of his travel. He is allowed to change as many trains as needed to reach the destination.
You need to find how many ways Codu can reach City B from City A.
Constraints
1 <= T <= 5
0 <= N <= 10^2Input
First line contains an integer T denoting the number of test cases.
Next T lines contains an integer N denoting the number of stations between A and B for each test case.
Output
For each test case print, no of combinations in a new line
Time Limit
1Examples
Input
2
0
1Output
1
2Explanation
For 0: No station between A and B. So only possible way to travel is by train1.
For 1: There is 1 station between A and B. So, Codu has two ways to travel. First way is to travel by train1 which halts at every station. Second way is to travel by train2 which starts from A and directly stops at B.
3) Relief Funds
Problem Description
An NGO wants to arrange funds for flood relief. It has divided volunteers into groups. A volunteer can only be a part of single group. Your task is to identify the members of the group which collects the maximum funds.
You will be given the funds collected by each volunteer and grouping pairs of the volunteers. You need group the volunteers through these pairs.
If there are more than one group, collecting maximum funds, then print the group having lesser members.
Constraints
0 < N, P <= 10000
0 < A, B <= NInput
First line contains one integer N, denoting number of volunteers.
Second line contains N space separated integers, representing the amount collected by each volunteer. The index of integer is the volunteer number starting from 1.
Third line contains the number of pairs, P.
Next P lines contain two space separated integers, A and B where A represents the first person and B represents the second person in the pair.
Output
One line containing M space separated integers, where each integer represents the volunteer number of the member in the group, sorted in ascending order.
Time Limit
1Examples
Example 1
Input
5
23 43 123 54 2
3
1 3
2 3
1 2Output
1 2 3Explanation
In the above example, we have five volunteer [1, 2, 3, 4, 5] who have collected [23, 43, 123, 54, 2] respectively.
We have three groups that consists of [1, 2, 3], [4], [5]. First group collects 189 units of money, second group collects 54 units of money and third group collects 2 units of money. Hence, the output is 1 2 3
Example 2
Input
5
10 10 10 15 15
3
1 2
1 3
4 5Output
4 5Explanation
In the above example, we have five volunteer [1, 2, 3, 4, 5] who have collected [10, 10, 10, 15, 15] respectively.
We have two groups that consists of [1, 2, 3], [4, 5]. First group collects 30 units of money and second group collects 30 units of money. But since, both groups collects the same amount. The output will be 4 5 as this group has lesser number of members.
4) Bus Travel
Problem Description
Amidst stiff competition the transport operators in the city are not in a position to increase the bus fare. One such public transport operator is you, who is suspecting some revenue loss despite the popularity of the bus service. Your reliable sources tipped you off that there are some passengers who take the advantage of overly crowded buses and take partial tickets (They take a ticket from a bus stop which is later than their actual start stop; or they exit bus much later than their destination stop on their ticket). Thanks to the in-out sensors you placed at the bus entry and exit gates which provides you the exact details of the traveler’s journey. Your objective is to find the bus stops from which these kinds of malpractices occur. You have to find out which passengers travelled with invalid tickets, and when they have over travelled (OT) or under travelled (UT).
A passenger is said to have over travelled if he does not have a valid ticket for all portions of his travel. Similarly, if a passenger has a valid ticket but alights the bus before his actual destination then he is said to have under travelled.
You have the data about every passengers’ source and destination at which they boarded and alighted the bus respectively. You also have data about how many tickets were issued from which source to which destination. Using this information, you have to find out the passengers who OT or UT. For this purpose, you will have to adopt a ticket allocation policy which will map a ticket to a given passenger. Rules of ticket allocation policy in order of their importance are mentioned below. They have to be applied sequentially to do the ticket to passenger mapping.
1. For all tickets whose source and destination match with passenger data i.e., the stops at which they boarded and alighted should be allocated first. Passenger order is preserved for ticket allocation i.e. First matching ticket is allocated to the person who boarded first. Refer Example 1 in the examples section to get a better understanding.
2. For all tickets whose source matches with the source stop in the ticket data, try and do allocation if possible.
3. For all tickets whose destination matches with the destination stop in the ticket data, try and do allocation if possible.
4. If neither source nor destination data matches with any tickets data, then sequentially allocate the remaining tickets in the order of passenger boarding.
For better understanding, please refer to example section.
Note:
. None of the passenger can travel in the same bus again
. Assume none of the passenger will get ticket before boarding
. Assume passenger names are unique
Constraints
0 < N < 50
0 < T < 100Input
– First line contains an integer N denoting the number of bus stops in a bus journey.
– Next N lines contain a string which provides passenger boarding and alighting information per stop. Format is as follows:
. There is an alphabetical string containing a pipe (|) character. The left-hand side of the pipe provides names of passenger boarding the bus and the right-hand side provides names of passengers alighting the bus.
. Passenger names are space delimited.
. When no passengers have boarded or alighted at a bus stop it would be denoted by (-).
– Next line contains an integer T denoting the total number of tickets issued.
– Next T lines contain two space delimited integers which denotes source and destination of each ticket respectively.
Output
Print the output in lexicographically sorted order of passenger names.
Each line of output should contain four things:
. First output will be passenger name
. Second output will be a number corresponding to start bus stop number
. Third output will be a number corresponding to end bus stop number
. Print “UT” if the travel type is under travel or “OT” if the travel type is over travel
OR
Print “VALID TRAVEL” when all the tickets are valid.
Time Limit
1Examples
Example 1
Input
4
A B | -
C | -
- | A B
- | C
3
1 3
1 2
2 3Output
B 2 3 OT
C 3 4 OTExplanation
Here we have 4 bus stops and 3 passengers (A, B, C).
A and B have boarded from bus stop 1 and nobody has alighted at bus stop 1.
C has boarded from bus stop 2 and nobody has alighted at bus stop 2.
Nobody has boarded from bus stop 3 and A & B has alighted at bus stop 3.
Nobody has boarded from bus stop 4 and C has alighted at bus stop 4.
Total 3 tickets are issued.
First, A is allocated ticket #1 with source 1 and destination 3 because source and destination are matching.
Then, B is allocated ticket #2 with source 1 and destination 2 because only source is matching. B has alighted at stop 3. So, B has over traveled from 2 to 3.
Then, C is allocated ticket #3 with source 2 and destination 3 because only source is matching. C has alighted at stop 4. So, C has over traveled from 3 to 4.
Hence the output is printed in lexicographically sorted order of passenger name as depicted above.
Example 2
Input
5
A B R | -
C | B
D | A C
- | D
- | R
5
1 2
1 4
2 4
2 3
3 4Output
A 3 4 UT
R 1 2 OT
R 4 5 OTExplanation
Here we have 5 bus stops and 5 passengers (A, B, C, D, R).
A,B and R has boarded from bus stop 1 and nobody has alighted at bus stop 1.
C has boarded from bus stop 2 and B has alighted at bus stop 2.
D has boarded from bus stop 3 and A & C has alighted at bus stop 3.
Nobody has boarded from bus stop 4 and D has alighted at bus stop 4.
Nobody has boarded from bus stop 5 and R has alighted at bus stop 5.
Total 5 tickets are issued.
First, B is allocated ticket #1 with source 1 and destination 2 because source and destination are matching.
Then, C is allocated ticket #4 with source 2 and destination 3 because source and destination are matching.
Then, D is allocated ticket #5 with source 3 and destination 4 because source and destination are matching.
Then, A is allocated ticket #2 with source 1 and destination 4 because only source is matching. A has alighted at stop 3. So, A has under traveled from 3 to 4.
Now, R is allocated remaining ticket i.e., ticket #3 with source 2 and destination 4. R has boarded from bus stop 1 and alighted at bus stop 5. So, R has over traveled from 1 to 2 and 4 to 5.
Hence the output is printed in lexicographically sorted order of passenger name as depicted above.
Click here for next 4 questions


